本文最后更新于:2022年8月25日 下午
UPD 2022/7/4:删除了一大堆没有意义的内容。
Definition
拓扑排序是什么?
就是在一个 DAG 上边,将所有的点排成一个线性的序列,使得每个点的起点都在终点前边。
那它可以用来干什么呢?
这可以用来处理一些层次关系,就是如果你想做事件 $A$,必先处理完事件 $B$,类似这样的关系。
实现
我们用 BFS 来处理拓扑排序。
我们拿这张图举例:
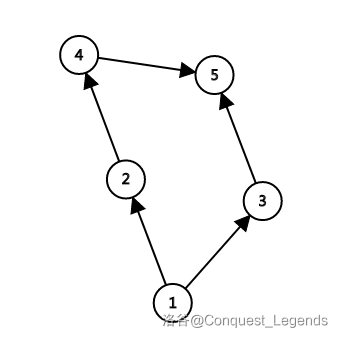
根据所有的起点都要在终点前边这句话,我们首先要找到入度为 0 的点进行我们的拓扑排序。
这张图的拓扑序也就是:
其中,2 和 3 的位置可以调换。
那么,我们就可以给这个图来个 BFS,每次看看这个点入度是否为 0,然后先把入度为 0 的点扔进队列。接下来输出这个点,然后开始遍历这个点所到达的每一个点,将到达的点的入度减一(即:删去这条边),然后看一看到达的点的入度是否为 0,如果为 0 就压进队列,然后重复上面的过程直到队列为空。
这边强烈建议看着思路写出来,不要看接下来的代码,因为这就是最简单的拓扑排序的模板,写出来是很简单的。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
| #include <cstdio>
#include <algorithm>
#include <queue>
#define N 100005
using namespace std;
queue <int> q;
int n, m, in[N];
struct Graph {
int y, nxt;
}e[N];
int ltp, lk[N];
int read() {
int x = 0, w = 1;
char c = getchar();
while(c < '0' || c > '9') {
if(c == '-') {
w = -1;
}
c = getchar();
}
while(c >= '0' && c <= '9') {
x = x*10+(c-'0');
c = getchar();
}
return x * w;
}
void write(int x) {
if(x < 0) {
x = -x;
putchar('-');
}
if(x > 9) {
write(x / 10);
}
putchar(x % 10 + '0');
}
void insert(int u, int v) {
e[++ltp] = (Graph){v, lk[u]};
lk[u] = ltp;
}
void top_sort() {
while(!q.empty()) {
int p = q.front();
q.pop();
write(p);
putchar(' ');
for(int i=lk[p]; i; i=e[i].nxt) {
int y=e[i].y;
in[y]--;
if(!in[y]) {
q.push(y);
}
}
}
}
void inp() {
n = read(), m = read();
while(m--) {
int u = read(), v = read();
insert(u, v);
in[v]++;
}
}
void work() {
for(int i=1; i<=n; i++) {
if(!in[i]) {
q.push(i);
}
}
top_sort();
}
int main() {
inp();
work();
return 0;
}
|
使用拓扑排序判环
如果给你的图不是个 DAG,那怎么办呢?
既然他有环,我们就得看看它是不是存在环,如果存在我们就得反映出来。
来个图:
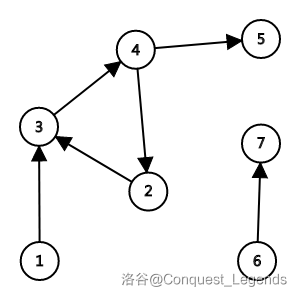
其实也简单,你会发现 2 3 4 组成的环会把一些点重复弹出队列。
根据这个性质,你每次把一个数弹出队列的时候就把弹出次数自增,最后看看是不是和结点数一样就可以了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
| #include <cstdio>
#include <algorithm>
#include <queue>
#define N 100005
using namespace std;
queue <int> q;
int n, m, in[N];
struct Graph {
int y, nxt;
}e[N];
int ltp, lk[N];
int ans[N];
int cnt, pos;
int read() {
int x = 0, w = 1;
char c = getchar();
while(c < '0' || c > '9') {
if(c == '-') {
w = -1;
}
c = getchar();
}
while(c >= '0' && c <= '9') {
x = x*10+(c-'0');
c = getchar();
}
return x * w;
}
void write(int x) {
if(x < 0) {
x = -x;
putchar('-');
}
if(x > 9) {
write(x / 10);
}
putchar(x % 10 + '0');
}
void insert(int u, int v) {
e[++ltp] = (Graph){v, lk[u]};
lk[u] = ltp;
}
void top_sort() {
while(!q.empty()) {
int p = q.front();
q.pop();
ans[++pos] = p;
cnt++;
for(int i=lk[p]; i; i=e[i].nxt) {
int y=e[i].y;
in[y]--;
if(!in[y]) {
q.push(y);
}
}
}
}
void inp() {
n = read(), m = read();
while(m--) {
int u = read(), v = read();
insert(u, v);
in[v]++;
}
}
void work() {
for(int i=1; i<=n; i++) {
if(!in[i]) {
q.push(i);
}
}
top_sort();
if(cnt == n) {
for(int i=1; i<=pos; i++) {
write(ans[i]);
putchar(' ');
}
} else {
printf("Leave me alone");
}
}
int main() {
inp();
work();
return 0;
}
|
拓扑排序的时间复杂度是 $O(n +m)$,挺快的。

