本文最后更新于:2022年8月25日 下午
大坑,填起来比较辛苦,可能慢点。
一直没时间写,估计抽个集训的空就完成了。
比较毒瘤,食用前请确保基础数据结构掌握得差不多了,不然回去学完线性表再来()
乱入的优先队列
一句话优先队列:往一个队列里边扔数,它自动给你排好序等你使用。
来一个十分简(bian)单(tai)的例题:
给定一个正数序列,求第 $k$ 小的子区间和。
$n \le 100000$
你跟我讲你不知道什么是子区间……
扫盲工作有了大进展。
懵了没有?我早就料到了哈哈哈,你的招式不过如此!
请先克制住把我按在地上暴揍的心理,现在我把这题做法告诉你你的招式不就也上来了嘛。
首先分析题目性质:这个序列是正数。
正数!正数!正数!
也就是说,我们选一个长度小的区间的和肯定比长度大的区间的和要小。
最小的,一定就是形如 $[i, i]$ 这样的区间了。
(都学到这了还不知道左闭右开和左闭右闭就去自闭吧)。
记 $S[l, r]$ 为区间 $l \to r$ 的和。
你一定看得出:$S[l-1, r] \ge S[l, r]$, $S[l, r+1] \ge S[l, r]$。
我们掏出一个堆,先加进去 $[1, 1] \dots [n, n]$ 区间和。
找到一个最小的,然后从这个区间去像上面的左右拓展,找出第二小的区间,以此类推。
记住疯狂塞到堆里边。
最后记住,来个 $\mathtt{map}$ 和 $\mathtt{pair}$ 的联动,去重用,我们不能计算重复的区间。
你要代码?我都写这么清楚了居然还要代码!
好吧……既然你们仍然是一脸懵逼,我还是写一下吧:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
| #include <cstdio>
#include <queue>
#include <algorithm>
#include <utility>
#include <map>
#define N 100005
using namespace std;
struct Node {
int l, r;
long long sum;
Node(int l, int r, long long sum) : l(l), r(r), sum(sum) {}
bool operator < (const Node &a) const {
return sum > a.sum;
}
};
int n, a[N], k;
map <pair <int, int>, bool> ds;
priority_queue <Node> q;
void inp() {
scanf("%d%d", &n, &k);
for(int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
q.push(Node(i, i, a[i]));
}
}
void work() {
while(k--) {
Node t = q.top();
q.pop();
if(ds[pair <int, int> (t.l, t.r)]) {
k++;
continue;
}
ds[pair <int, int> (t.l, t.r)] = true;
if(t.l != 1) {
q.push(Node(t.l - 1, t.r, t.sum + a[t.l - 1]));
}
if(t.r != n) {
q.push(Node(t.l, t.r + 1, t.sum + a[t.r + 1]));
}
printf("%d %d %d\n", t.l, t.r, t.sum);
}
}
int main() {
inp();
work();
return 0;
}
|
前缀和与差分
前缀和是什么?
一个序列,定义一个 $pre$ 数组,$pre[i]$ 为前 $i$ 个数的和,查询一个区间 $[l, r]$ 的时候,只需要 $pre[r] - pre[l - 1]$。
那这玩意如何计算呢?
异常简单:
1
2
3
| for(int i = 1; i <= n; i++) {
pre[i] = pre[i - 1] + a[i];
}
|
二维的东西……这东西是需要画图的,不过我觉得脑补应该可以吧……如果你非要看图(我是不会画的)就使用 gfs(google first search)。
差分又是什么呢?
差分数组的定义:
差分能干什么?
比如说:
有些东西直接统计起来,凉凉 TLE。
但是如果具有可减性,就可以使用差分来降低时间复杂度。
完美。
树状数组
现在,我给定一个序列,需要您写出一个数据结构,支持以下操作:
- 在第 $x$ 的位置上加上 $y$。
- 给出 $x$ 的前缀和。
现在该如何是好呢?
如果您使用数组,您得先统计一遍前缀和,恭喜您,我修改了序列,于是您又去改一遍前缀和,然后我接着修改序列……
有常识的人都知道,TLE 在所难免了。
这种数据结构需要什么特点?
- 树形结构的每个节点表示一个子集。
- 为了高效修改,每个序列上的位置只出现在少数个树形结构的节点上。
- 为了查询高效,对任意查询,可以通过少数个树形结构的节点拼出来。
那么,有没有数据结构能来就我们一命?
树状数组可以满足您的要求。
树状数组是个什么东西?
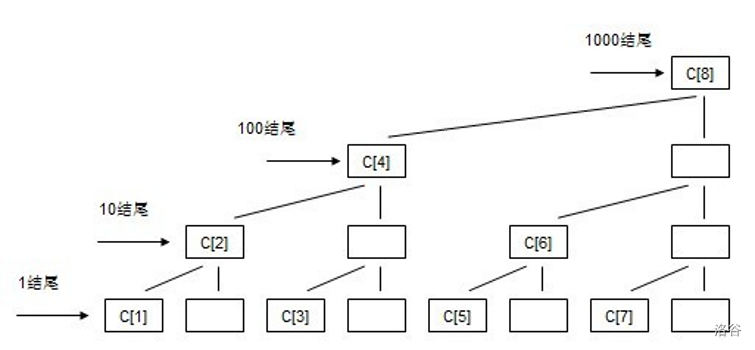
剑鱼这东西实在毒瘤,于是我盗了 noip 的图,不过这是我氪了金的应该算是正常使用吧……
假设一个序列:$A[1] \sim A[8]$,用 $C[]$ 表示树状数组。
$C[x]$ 表示 $A[x - 2^k + 1, x]$ 这个区间的和,$k$ 是表示 $x$ 的二进制表示中第一位的 1。
蛤?
比如说,6,二进制表示 110。
则,k 就是 1。$2^k$ 就是 2。
那么这玩意怎么求呢?难不成我还要去位运算?
恭喜您,答对了,给您加 10 分。
极其简单,一句话就可以求出 $2^k$:
我们如何去构建一个树状数组?
根据我们之前说过的一堆东西,我们可以提前根据我们手中的数据数组去构造。
1
2
3
4
5
6
7
8
| void build(int c[]) {
memset(c, 0, sizeof(c));
for(int i=1; i<=n; i++) {
for(int j=i-lowbit(i)+1; j<=i; j++) {
c[i] = c[i] + t[j];
}
}
}
|
我们查询一个前缀的和,可以用 $O(\log n)$ 个树状数组的节点拼起来,然后成功拼出这个前缀。
求法:
1
2
3
4
5
6
7
8
| int sum(int x) {
int ans = 0;
for(int i=x; i; i-=lowbit(i)) {
s += c[i];
}
return ans;
}
|
在 $x$ 的位置上加上 $y$。
你会发现,在 $x$ 前面的结点是不会收到影响的,只有后面的结点才会被影响。
存储输入数据的数组好说,直接一加就行了,但是树状数组里边怎么办呢?
因为之前的和它半毛钱关系都没有,我们直接从 $x$ 和它以后的那些点进行修改就可以了。
1
2
3
4
5
6
| void modify(int x, int y) {
t[x] += y;
for(int i=x; i<=n; i+=lowbit(i)) {
c[i] += y;
}
}
|
树状数组就这么点东西了。
P3374,模板题。
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
| #include <cstdio>
#include <cstring>
#define N 500005
using namespace std;
int c[N];
int n, t[N], m;
int lowbit(int x) {
return x & -x;
}
int find(int x) {
int ans = 0;
for(int i=x; i; i-=lowbit(i)) {
ans += c[i];
}
return ans;
}
void modify(int x, int y) {
t[x] += y;
for(int i=x; i<=n; i+=lowbit(i)) {
c[i] += y;
}
}
void init(int c[]) {
memset(c, 0, sizeof(c));
for(int i=1; i<=n; i++) {
for(int j=i-lowbit(i)+1; j<=i; j++) {
c[i] = c[i] + t[j];
}
}
}
void inp() {
scanf("%d%d", &n, &m);
for(int i=1; i<=n; i++) {
scanf("%d", &t[i]);
}
}
void work() {
init(c);
for(int i=1; i<=m; i++) {
int opt, x, y;
scanf("%d%d%d", &opt, &x, &y);
if(opt == 1) {
modify(x, y);
} else {
printf("%d\n", find(y)-find(x-1));
}
}
}
int main() {
inp();
work();
return 0;
}
|
